Last Time

ToDoList :

Timeline

2019/09/02-2019/09/08

2800-3800

JAG 2009 E Symmetry
2017 SEERC Divide and Conquer
上海网络赛 Counting Sequences II
2018 ICPC 北京 G Solving Equations is Easy

2500-2700

沈阳网络赛 Special necklace
沈阳网络赛 Ghh Matin
沈阳网络赛 Gugugu’s upgrade schemes

2100-2400

2019/09/02-2019/09/08

2800-3800

ICPC 2018 徐州 D Rikka with Subsequences
ICPC 2018 徐州 I Rikka with Sorting Networks
2019 徐州网络赛 F Little M’s attack plan
JSOI 2018 战争
SCOI 2015 小凸想跑步

2500-2700

2100-2400

2019/08/12-2019/08/19

2800-3800

2018多校9 E Rikka with Rain
牛客10 G Road Construction
UVA 1017 World Finals 2002 Merrily, We Roll Along!
POJ 1418 Viva Confetti
POJ 3384 Feng Shui

2500-2700

2100-2400

2019/08/05-2019/08/11

2800-3800

ICPC 2018 北京 Rikka with Triangles
ICPC 2018 徐州 Rikka with Illuminations
SRM 595 Constellation(Hard)
SRM 573 WolfPack(Hard)
SRM 750 PurpleSubsequences(Hard)

2500-2700

2100-2400

2019/07/29-2019/08/04

2800-3800

杭电4 E Good Numbers
杭电4 F Horse
牛客5 F maximum clique 1

2500-2700

杭电4 C Divide the stones
牛客6 E Androgynos
牛客5 C generator 2
牛客5 E independent set 1
牛客5 I three points 1

2100-2400

2019/07/22-2019/07/28

2800-3800

ABC 134 F Permutation Oddness
SRM 648 Fragile(Hard)
SRM 633 GCDLCM(Hard)
388E Fox and Meteor Shower(3000)
528E Triangles 3000(3000)

2500-2700

2100-2400

牛客4 D triples I

2019/07/15-2019/07/21

2800-3800

SRM 655 BichromeSky(Hard)
1146H Satanic Panic(2800)
1142C U2(2800)

2500-2700

1195F Geometers Anonymous Club(2700)
1194F Crossword Expert(2500)

2100-2400

1190D Tokitsukaze and Strange Rectangle(2200)
1194E Count The Rectangles(2200)
1188B Count Pairs(2200)
1195E OpenStreetMap(2100)

Topcoder

SRM 754

Medium

题意 : 给定投影等价类数，构造一组点集方案。
题解 : 两个点有两个等价类，对于一个点集，$n^2$条直线去重后的个数为等价类数。构造两列点即可。

Hard

题意 : 给定$4$连通块大小和$8$连通块大小，返回构造结果。
题解 : $8$连通块是由若干$4$连通块组合起来，状压DP一下，DP出一组解。然后按行构造即可。

SRM 753

Hard

题意 : 给定一个序列，区间询问去掉一个数后的最大异或和。
题解 : 可持久化Trie树，区间异或和在区间的Trie树上异或出最大值。

2019 Humblefool Cup Prelims

Hard

题意 : 定义相邻的两个质数为只有一个数位不同，且长度相同。询问两个质数可以到达。
题解 : 质数非常连通，预处理之后会发现，只有$4$个块，$2$个是孤点，还有$1$个是大小为$2$的块，剩下的点全部联通。

SRM 752

Hard

题意 : 有$n$个硬币在桌子上，有$1$个硬币在手里，每次抛硬币，正面的话桌面上加$1$个硬币，手里留$1$个硬币，如果桌上有$2N$个硬币则游戏结束。反面的话，从桌上硬币拿走手里的硬币数个放到手里，如果桌上拿空则游戏结束。输出期望场数。
题解 : 转移显然有环，但是由于正面的特殊性，定义$f[i]$表示手里$1$个硬币，桌上$i$个硬币的期望场数。转移方程$f[i]=(f[i+1]+1)*0.5+(f[i]+2)*0.5^2+(f[i-2]+3)*0.5^3+\cdots$。可以发现转移有后效性，但是我们可以将$f[i+1]$去除后效性。

SRM 750

Hard PurpleSubsequences

题意 : 给定一个长度为$n$的序列，询问最长上升子序列长度大于等于$L$的本质不同子序列个数。$n\le 60,x_i\le 20,L\le 6$
题解 : 本质不同先建出序列自动机，然后在上面大力DP。DP的过程中类似我们直接求解LIS的过程，把保存LIS长度为i的最后一个数字的数组保存在每个节点上。
$O(n^2S)$

SRM 655

Hard

题意 : $n$个红点，$m$个蓝点，没有三点共线，第i个红点以$p_i$的概率出现，求红点的凸包包含所有蓝点的概率。$n, m \le 100$
题解 : 对于包含所有蓝点的要求，等价于包含所有蓝点形成的凸包。对于一个红点，对蓝点构成的凸包做切线，这两条切线是这个红点的覆盖范围。问题就转化为有$n$个区间，每个区间出现的概率为$p_i$，询问全部覆盖的概率，DP一下即可。
复杂度$O(n^3)$。

SRM 648

Hard Fragile

题意 : 询问有$m$个桥的带标号的$n$个点的图的个数，$n\le 50, 0\le m\le n-1$。
题解 : 首先，我们可以先求出$n$个点$m$个桥的连通图个数，然后背包求答案即可。
然后，对于一个桥，断开之后就变为了两个联通图，所以我们考虑dp求出$f[i][j][k]$为$i$个点，$1$号点所在边双大小为$j$，桥的个数为$k$的方案数。
转移的时候还需要$n$个点的连通图个数，再dp一次求一下。
没有桥的情况拿任意的减去所有有桥的。
复杂度$O(n^5)$。
PS : 做的时候感觉好麻烦，翻了一下别人的，tourist就是dp的，petr打表了，50的数据范围真的是…

SRM 633

Hard GCDLCM

题意 : 给定四个数组$A,B,C,D$，构造一个数组$x$使得，当$D[i]=0$时，$C[i]=Gcd(x[A[i]],x[B[i]])$，否则$C[i]=Lcm(x[A[i]],x[B[i]])$。
$n\le 200, C[i]\le 10^9$
题解 : 这个感觉还不太难。由于$gcd=\Pi p_i^{min(cnt_a,cnt_b)}$，$lcm=\Pi p_i^{max(cnt_a,cnt_b)}$，那么对于$C[i]$，唯一分解得到幂次后，得到了$x[a]$和$x[b]$对于每个质因子的要求，记$x[i]$对质因子$p$的幂次为$cntX[i][p]$，拿gcd举例就是，$min(cntX[a][p],cntX[b][p])=cntD[i][p]$，可以拆成$cntX[a][p]=cntD[i][p]$且$cntX[b][p]\ge cntD[i][p]$或$cntX[a][p]\ge cntD[i][p]$且$cntX[b][p]=cntD[i][p]$。
2-sat判一下即可。
PS : 好久没写2-sat了，写完翻题解的时候翻到了姚老板的blog。

SRM 595

Hard Constellation

题意 : 给定$n$个点，以及他们出现的概率，询问构成凸包的期望面积。$n\le 50$
题解 : 考虑一个构成凸包内的点，他们出现不出现对于该凸包面积的概率不影响，那么只要考虑在边界的点即可。那么可以想到求凸包面积的方法，是每次求$OA_{i}A_{i+1}$的有向面积。所以枚举两个点，假设他们是凸包上的一条边，即某一侧没有任何点，计算概率。正反各求一次即可。
$O(n^3)$

SRM 573

Hard WolfPack

题意 : 给定$n$个点，每秒每个点可以往上下左右移动一步，询问$m$秒后走到同一个点的方案数。$n\le 50,m\le 10^5$
题解 : 对于一个点，每次可以$x+1/-1$，$y$不变，或者$y+1/-1$，$x$不变。这里$x$和$y$的变化是相关的，会互相影响，为了消除这种影响可以很自然想到欧几里得距离转切比雪夫距离。
那么我们将其变换后，每次移动变为$x+1/-1$，$y+1/-1$，这样两维就独立了。然后考虑移动到一个点的方案数，问题就是$n$个数轴上的点，每次左右走，询问$m$秒后走到同一位置的方案数。
随便取一个点，枚举$+1$的个数，然后计算其他点走到这个点的方案数。$x$和$y$分开求完乘起来即可。
$O(n^2m)$

TCO 2014 Round 1B

Medium WolvesAndSheep

贪心反例 :
x[]
[]v
纯贪心（按行和列分别做一次），不会分割，所以x还是能到达v。

Hard EagleInZoo

题意 : 给定一棵树，从根节点放入动物，如果这个节点已经有动物了，就等概率的选择子节点往下走，重复过程直到有空节点或离开树，一旦离开树，这次的过程停止。询问放入$m$个动物，最后一只留在树上的概率。
题解 : 关键 : 设计状态转移时，要让转移的方案不相交。
$dp[i][j]$表示以$i$为根的子树，放入$j$个动物，最后一只能够留在树上的概率。
转移的时候考虑最后一个动物留在哪个子树，这样使得转移的方案不相交。
假设以$i$为根的子树放入$j$个动物，$i$的子节点数为$c$，枚举进入某个个子树$ch$的动物数$k$，那么概率为${\frac{1}{c}}^{k}*(1-\frac{1}{c})^{j-1-k}*C_{j-2}^{k-1}$ 不管进入别的$ch$的情况是怎么样，所以概率是$1-\frac{1}{c}$

TCO 2014 Round 2A

Easy SixteenBricks

题意 : 给定16块$1*1*x[i]$砖，放在$4*4$的格子里，使得可以看见的面积最大。
题解 : 关键 : 首先要大小交替摆放，然后降维分析。
$a>b>c>d$，考虑一维情况$adbc$比$acbd$更优，因为两个的面积分别是$2a+2b-2d$和$2a+2b-2c$，然后放在二维即可。

Medium NarrowPassage

题意 : 在$0$到$l$的走廊里，给定每个物品$n\le 50$的初始位置和目标位置，要改变物品的顺序，必须这些物品在最左端或最右端，询问最小移动步数。
题解 : 关键 : 最优移动的方案。
首先一种情况是，按最开始的位置分成三段，左边一段全部移到最左边，右边一段全部移到最右边，中间一段自行调整。
这种情况的要求是，中间段不能交叉，左边和右边那段的目标位置不能跨越中间那段。
另一种方案是这类情况的最优方案是，按照起点排序，左边到左端点，右边到右端点，然后按终点排序，枚举边界，右边点的到右端点。

Hard TreePuzzle

题意 : 给定一棵树$(n\le 500)$，给定每个点有无黑点，根节点放一个红点，询问哪些点能被红点到达。
题解 : 关键 : 分类讨论啊。
首先，你现在红点在$x$，黑点分布为$f[x]$，$y$为$x$的一个子节点，判断$y$是否可达。
1.若$y$的子树中空节点数大于等于$1$，则可达。
2.若$y$的子树中空节点数等于$0$，且$x$的子节点中，子树中空节点数大于等于$1$的个数为$0$，即$x$的子树中无空节点，则不可达。
3.若$y$的子树中空节点数等于$0$，且$x$的子节点中，子树中空节点数大于等于$1$的个数大于等于$2$，则可达。
4.若$y$的子树中空节点数等于$0$，且$x$的子节点中，子树中空节点数大于等于$1$的个数等于$1$，记该节点为$z$，其子树中空节点数为$cnt$。
找到$z$的子树中离$z$最近的，且度数大于等于$3$的节点$z’$，若$cnt\ge z$到$z’$的节点数+$2$，则可到达，否则不可到达。

Atcoder

ABC 134

F Permutation Oddness

题意 : 对于一个长度为$n$的排列$P$，它的权值为$\sum_{i=1}^{n}|P_i-i|$。现在询问长度为$n$，权值为$m$的排列数。$n\le 50$。
题解 : 首先把这个权值转换一下。这个权值的构成可以看做是两个$1$-$n$顺序排列的匹配，权值为匹配两点的距离差，再转换一下可以看做在$i$和$i+1$($1\le i\le n-1$)中间画一条横线和匹配的线的交点个数。如图:

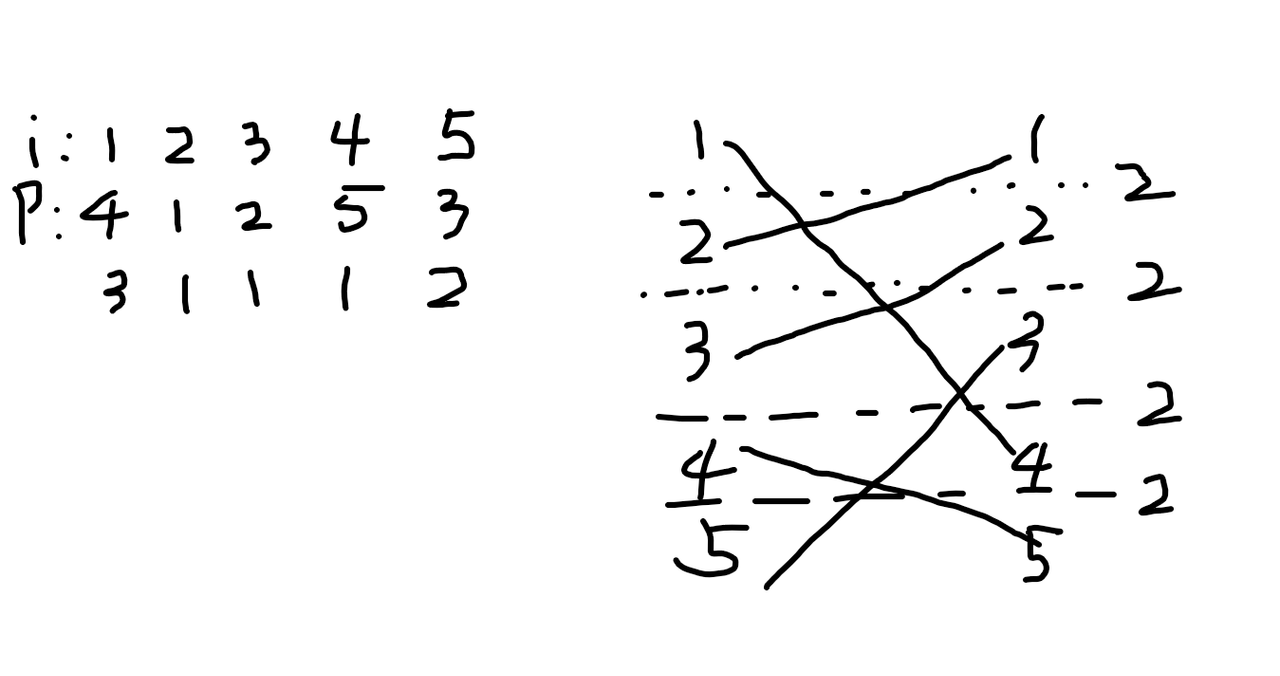
现在假设我们用左侧的点去匹配右侧的点，每次将左侧的点$i$和比它小的点匹配，和比它大的点匹配由另一侧的点来决定。由另一侧点来决定的点暂且视为闲置点。
假设我们现在匹配完前$i$位了，有$j$个闲置点(左右两侧各$j$个)，那么与$i$和$i+1$中间的直线相交的点的个数为$j$个。
根据这个我们就可以DP了。
$f[i][j][k]$表示前$i$位中有$j$位没有匹配，权值和为$k$的方案数。
$O(1)$转移，复杂度$O(n^4)$
PS : 这题放在ABC很大原因是OEIS能直接找到所有答案的表。所有日文题解都标了”箱根DP”，get不到这个点，但可能在日本已经人尽皆知了吧。
PPS : 有兴趣可以看看这个 https://arxiv.org/pdf/1202.4765.pdf

ARC 88

D Wide Flip

题意 : 给定一个长度为$n$的$01$序列，可以翻转一段连续的长度大于$k$的区间，询问最大的$k$。
题解 : 关键 : 假设我们选定了一个$k$，我们能单独修改某些单独位置。
修改第$i\ge k+1$位，可以通过修改$[1,i-1]$和$[1,i]$。
修改第$i\le n-k$位，可以通过修改$[i,n]$和$[i+1,n]$。
到了第$i$和$i+1$位为$01/10$时，我们要修改第$i$和$i+1$位都能达到我们的目的，所以取一个更大的$k$。
$0110010010$
$1\ \ 3\ \ 56\ \ 89\ \ $
$9\ \ 7\ \ 54\ \ 21\ \ $
可以观察上图，取$\lceil\frac{n}{2}\rceil$一定可以实现目的，因为可以随意修改左右两侧的值，实际上我们要去找的，最靠近中心的01交替的位置，以这个位置对称过去的两侧都可以随意修改，而剩下来中间的部分不用修改。

E Papple Sort

题意 : 给定一个字符串，询问通过交换相邻字符，最少几次能变为回文串。
题解 : 关键 :
1.a…a…a…a，第2个a一定不会越过第3个a，也就是说相同字母的相对位置不变。
2.交换相邻字符我们想到 : 1)可以转化为任意两个位置的交换2)统计答案为求目标位置的逆序对数。
现在转化为求目标位置，回文的话可以看成是一层一层的，结合第一点我们可以确定第1个a一定和最后一个a是一个回文对，然后我们考虑两对的情况。
a..a.b…b
a..b.a…b
a..b.b…a
分为上面三种，其中第三种显然最终a在b外面，第一种一定会先变成第二种。
而第二种,首先我们假设中间的b和a关于中心对称了，因为不对称要整体平移对于ab谁在外面无影响，然后a在外面我们要右侧a移到右侧b外面，b在外面我们要左侧b移到左侧a外面，因为要对称这两个的操作数是相同的。
所以根据上面三种情况，我们从左向右扫标记每对最终的位置，求一个逆序对即可。

ARC 89

D Checker

题解 : 关键 : 把每个位置的横纵坐标对$2k$取模。
做二维前缀和即可。

ARC 90

E Avoiding Collision

题意 : 给定一张无向图，给定两个点$s$和$t$，两个人分别从$s$和$t$出发，并且都沿着最短路走到$t$和$s$，询问两个人不相遇的方案数。
题解 : 核心是容斥来求，$ans=$最短路对数-到达同一个点的最短路对数-到达同一条边的最短路对数。
先分别求出$s$和$t$到每个点的距离$dis_{1/2}[i]$和最短路方案数$num_{1/2}[i]$，最短路对数为$num_{1}[t]^2$，枚举点，若能作为最短路上的点且两人到达时间相同则计入，枚举边，若能作为最短路上的边且两人在边上能够相遇则计入。

F Number of Digits

题意 : 定义$f(a)$为$a$在十进制中的位数，给定$S(S\le 10^8)$，询问有多少对$l,r$满足，$\sum_{i=l}^{r}f(i)=S$。
题解 : 首先想到$\text{two-point}$，但是$l,r$的范围很大不适用，但但是我们注意到一个关键的性质，当$l\ge10^7$时，因为$f(i)\ge8,i\in[l,r]$，$l$到$r$的距离小于等于$\frac{S}{8}$，所以会得到$f(r)\le f(l)+1$。我们分情况来看一看。
$1.f(l)=f(r)$，此时要求$f(l)|S$，方案数为$9*10^{f(l)-1}-\frac{S}{f(l)}+1$。
$2.f(l)+1=f(r)$，令$t=r-l+1$，$f(l)=\text{len}$，$f(r)=\text{len}+1$，$l$到跨越的距离为$x$，跨越到$r$的距离为$y$，得到等式$S=\text{len}*t+y$，枚举$t$，则$y=S\%t$，$x=t-S\%t$，若$x，y$都大于$0$则计入答案

Codeforces

Codeforces Round #574

1195F Geometers Anonymous Club

题意 : 给定$n$个凸包，有$m$次询问，查询在$[l_i,r_i]$中的凸包的闵可夫斯基和的点集大小。
题解 : 回想一下合并两个凸包求闵科夫斯基和的过程，会发现相同斜率的线段只用一次，所以问题转化为求区间中颜色个数，离线树状数组即可。

1195E OpenStreetMap

题意 : 询问在$n\cdot m$的矩阵中，所有$a\cdot b$的子矩阵的最小值的和。$n,m,a,b\le 3000$。
题解 : 先单调栈求一遍每个点横着往左长度为$a$的最小值，再用这个最小值为权值纵向求一个长度为$b$的，最后全加起来即可。$O(nm)$。

Educational Codeforces Round 68

1194F Crossword Expert

题意 : 有$n$个任务，第$i$个任务的完成时间为$t_i$，Bob完成每个任务的时间等概率地为$t_i$或$t_i+1$。现在Bob按顺序完成任务，询问在$m$的时间里，期望完成多少任务。$n\le 2\cdot 10^5, 1\le t_i\le 10^9, m\le 2\cdot 10^{14}$。
题解 : 对于第$i$个任务，完成它的概率为$\frac{\sum_{j=0}^{m-sum[i]}C_{i}^{j}}{2^i}$。
对于$\sum_{j=0}^{a}C_{i}^{j}$转移到$\sum_{j=0}^{a}C_{i+1}^{j}$，可以使用$\sum_{j=0}^{a}C_{i+1}^{j}=2\cdot\sum_{j=0}^{a}C_{i}^{j}-C_{i}^{a}$来实现。
且由于$m-sum[i]$是下降的，所以可以只用求$O(n)$个组合数即可。

1194E Count The Rectangles

题意 : 给定$n$条平行于x轴或y轴的线段，求一共能围成多少个不同的矩形。$n\le 5000$。
题解 : 把$x$轴平行的线按$y$排序，将$y$轴平行的线拆成两个点(入点和出点)，并按$y$轴排序。
枚举一条$y$轴平行的线，将所有$y$值小于它的点的$x$值加入或删除(入点和出点)，然后按$y$值遍历大于这条平行于$x$轴的线，将$x$值插入和删除，每次查询在这两条平行于$x$轴的线中间合法的$x$值数量即可。$O(n^2\log{n})$。

Codeforces Round #573

1190D Tokitsukaze and Strange Rectangle

题意 : 给定$n$个点，每次使用一个凹字形的框框出一个点集，询问本质不同的点集个数。$n\le 2\cdot 10^5$。
题解 : 先把所有点按$y$轴排序，从大到小，每层统计新加入的点与原来的点形成的贡献，每层结束再把新点加进去。离散化和树状数组处理统计贡献即可。

Codeforces Round #572

1188B Count Pairs

题意 : 给定$n$个值$x_i$，询问有多少对在模$p$意义下满足$(x_i-x_j)\cdot(x_i^2+x_j^2)=k$。$n\le 3\cdot 10^5$
题解 : 上面的式子乘$x_i+x_j$变为$x_i^4-x_j^4=k(x_i-x_j)$，移项得到$x_i^4-x_i\cdot k=x_j^4-x_j\cdot k$。map处理一下即可。
$O(n\log{n})$

Forethought Future Cup - Elimination Round

1146H Satanic Panic

题意 : 给定平面上$n$个点，询问形成的五角星数量。$n\le 300$
题解 : 这题有个DP做法，我这里写个组合的。
首先是$C_{n}^{5}$，考虑减掉不合法的情况。
形成合法五角星的5个点，肯定是每个点都在这5个点形成的凸包定点上。
所以，可以分为两种情况：三角形中有两个点，四边形里有一个点。
第一种情况，枚举一个三角形，内部拿两个即可。
第二种情况，枚举一个三角形，在内部拿一个点，外部再拿一个点即可。
可以使用bitset的与和count来求三角形内点的个数。
$O(n^3)$

Codeforces Round #549

1142C U2

题解 : 给定$n$个点，任意两个$x$值不同的点可以求出一个满足$x^2+bx+c=y$的抛物线。询问没有任何点严格在抛物线上方的抛物线个数。$n\le 10^5$。
题意 : 对于一个点$(x_i,y_i)$和他所在的抛物线$x^2+b_ix+c_i=y$，要求满足不存在$y’>x’^2+bx’+c$，这个点所在的抛物线可以表示为$bx_i+c=y_i-x_i^2$，$x_i,y_i$已知，而$b,c$未知，可以将$b,c$看做未知数，每个点转化为$(x_i,y_i-x_i^2)$后可以表示为这条直线上的点，那么任意两个转化后的点的连线就是这条直线。
按照抛物线的要求，要求这条直线上面没有点，即求上凸包。
注意$x$轴值相同的点不算上凸包的点。
$O(n\log{n})$

Codeforces Round #296

528E Triangles 3000

题意 : $n$条直线，等概率挑选$3$条，求围成三角形面积的期望。$n\le 3000$
题解 : 考虑怎么求构成的所有三角形的面积。
对于三角形的三个顶点逆时针为$A,B,C$，面积可以写为$(OA\times OB+OB\times OC+OC \times OA)/2$，同时这三个点都是交点，那么也就可以转化为，枚举一条直线，直线上的所有交点做叉积即可。
然后对于$OA\times OB+OA\times OC=OA\times(OB+OC)$，极角排序保证逆序，前缀和来维护即可。

Codeforces Round #228

388E Fox and Meteor Shower

题意 : 给出$n$颗流星在$t1$秒和$t2$秒的位置，询问能找到最多多少颗流星，使得两两相交。$n\le 1000$
题解 : 做的时候没感觉到居然是个讨论题。首先可以看做是个三维直线，那么两两相交的集合就是 : 直线交于同一点或者同一平面且不平行
存到Map里，注意细节。

Educational Codeforces Round 63

F Delivery Oligopoly

题意 : 给一张$n(n\le 15)$个点，$m$条边的双连通图。询问删除最多的边使得新图为双连通图的方案。
题解 : 对于一个双连通图，双连通块的构造方法是一个双连通块加上一条链/一个点。那么我们枚举双连通块点集$s$，枚举一个端点为$i,j$且点集为$t$的链，使得$i,j$分别与$s$内两点相连。
预处理出$i$到点集$s(i\not\in s)$的最大/次大距离，预处理出点集为$s$，左右端点为$i$和$j$的链的最小花费。转移记录方案。
复杂度$O(3^n\cdot n^2)$。

多校

杭电4

C Divide the stones

题意 : 给定重量为$1$-$n$的石头，要求分成重量相等，数量相同的$m$组。$n\le 100000,\sum n\le 500000,m|n$
题解 : 每堆石子$\frac{n}{m}$个，重量为$\frac{n(1+n)}{2m}$。
分情况讨论，如果$2m|n$，那么两头取即可。否则，除去等于1的情况，$\frac{n}{m}$可以写成$3+a$且$2|a$的形式。这时先构造一个将$1$-$3m$放入$m$组，每组$3$个，再把剩下的放进去即可。

D Enveloping Convex

E Good Numbers

题意 : 定义一个数是好的，为$8$进制下每个数码出现次数是$3$的倍数，且该数为$p$的倍数。询问八进制下长度为$n$的好的数有多少。$n\le10^{18},p<8$
题解 : $f[i][j][k]$表示长度为$i$，每个数码出现次数模$3$的次数，在模$p$下的余数$k$。
BM+打表

F Horse

题意 : 初始能量为$0$，现在要越过$n$棵树，高度为$h_i$，越过一棵树能量减少$h_i$，得到收益为当前能量值。
在越过树前，可以把树吃掉，树的高度变为$0$。
在越过树后，可以休息，恢复能量值为吃掉的所有树的高度和。
最多$m$次休息，$t$次吃树，询问最大收益值。
$n\le10000,m,t\le50,h_i\le10000$
题解 : 可以发现，得分只在跨越树，休息时能量重置。
现在，我们考虑得分是怎么构成的。对于第$i$棵树，它的得分为 : 上一次休息前吃的树高和$-$上次休息后没吃的树高和$=$上一次休息前吃的树高和$-($上次休息后的树高和$-$上次休息后吃掉的树高和$)=$前$i$棵树中吃掉的树高和$-$上次休息后到$i$的树高和。
这两部分就可以分开计算了。
第一部分，是选择$t$个$h_i$使得$\sum{h_i*(n-i+1)}$最大。
第二部分，是将序列最多分为$m+1$段，使得每段的权值和最小，区间$l,r$的权值为$\sum_{i=l}^{r}h_i\cdot(r-i+1)$。
第一个直接做，第二个是决策单调的。

牛客6

E Androgynos

题意 : 构造点数为$n$的自补图。
题解 : 当$n=4m$或$4m+1$时有解。
$n=4m$时，将$n$个点等距放在一个圆上，从$1$开始标号，奇数点每次向接下来的$[1,m]$点连边。偶数点向后面的$[m+1,2m]$点连边。映射为每个点标号后移一位。
$n=4m+1$时，在$n-1=4m$的连边中，偶数点度数比奇数点度数小$1$，将$n$与偶数点连边即可，$n$映射不动。

F K-ary Heap

题意 :
题解 :

牛客5

C generator 2

题意 : $f_i=a\cdot f_{i-1}+b\cdot f_{i-2}$，求$f_n$。$n\le 10^{10^{6}}$
题解 : 10进制快速幂。复杂度$O(4\log{n})$

E independent set 1

题意 : 给定一个$n$个点$m$条边的图，询问所有子图的最大独立集之和。$n\le26$
题解 : 对于一个点集$s$，最大独立集的转移分为，去掉一位和去掉一位的相邻点。
这一位每次选择末位即可包含全部情况。
复杂度$O(2^n)$

F maximum clique 1

题意 : 给定$n$个正整数$x_i$，选出一个集合$S$，满足任意两个数二进制下至少两位不同，询问最大$|S|$。$n\le 5000,x_i\le 10^9$
题解 : 按题意建图是求最大团，最大团和最大独立集是互补的，所以把条件反过来建立补图，即任意两个数二进制下最多一位不同，由于是集合任意两数不同，所以是任意两数二进制下只有一位不同。
证明该图是二分图，等价于证明没有奇环。考虑一个数$a$所在的环为奇环，该环上的点$x$与$a$的不同位数记为$f(x)$。$a$邻接的两个环上的点$f(x)$都为$1$，每次走一步可以使得$f(x)$加一或减一，且$f(x)$永远不为$0$，所以环长不为奇数，所以是二分图。按1的个数的奇偶也很好证。
求二分图最大独立集即可。
每个点有一位不同的点最多$30$个，所以边数为$30n$，复杂度$O(30n^2)$
输出方案时，输出左侧未匹配点和右侧匹配点。做完二分图匹配后再将所有左侧未匹配点dfs一次，右侧没有被遍历到的点就是合法点。

I three points 1

题意 : 给定三角形边长，将其放入给定的矩形中，输出一组解。
题解 : 别写什么swap了，排列就完事了。

牛客 4

D triples I

题意 : 询问$n$由最少几个三的倍数或起来得到，输出方案。
题解 : 题目保证输入都有解，那么如果不是三的倍数最少就是2个数。
$f[i][j][k]$为前$i$位，第一个数模3的为$j$，第二个数模3的为$k$的解。
DP比直接做会多个10的倍数。

Regional

ICPC 2018 北京 Rikka with Triangles

题意 : 给定$n$个点，询问锐角三角形个数和总面积。$n\le2000$，坐标范围$\le10^{18}$
题解 : 首先，锐角三角形不好判断，为什么？比较一下三种三角形，锐角三角形三个角都是锐角，直角三角形和钝角三角形只有一个角是非锐角，所以我们考虑反着求。
首先，求钝角三角形个数和直角三角形个数。枚举一个点求以这个点为钝角/直角，然后极角排序，满足为大于/等于90度且小于180度的点可以双指针来统计。$O(n^2logn)$
其中，$C_{n}^{3}$中会包括三点共线的情况，也要统计。枚举一个点，极角排序，统计$[0,\pi)$的三点共线。$O(n^2logn)$
面积还是考虑求钝角和直角三角形的面积。和CodeForces 528E Triangles 3000的思路一样，钝角和直角，极角排序，双指针，前缀和优化。总面积和就是528E。$O(n^2logn)$
这里面极角排序用象限和叉积，使用全整数，__int128。

ICPC 2018 徐州 D Rikka with Subsequences

题意 : 给定一个字符串，询问每个合法子序列出现次数的立方和。$n\le 200$
题解 : 立方和可以转化为3个字符串匹配次数。然后就有一个DP的方法，设$f[i][j][k]$为三个串分别到$i,j,k$且三个位置都相同的方案数，$f[i][j][k]=\sum f[i’][j’][k’]*mp[x[k’],x[j]]$。
然后拆成三个前缀和，分别前缀和维护即可。
复杂度$O(n^3)$

ICPC 2018 徐州 I Rikka with Sorting Networks

题意 : 给定$m$个排序网络，询问有多少排列，在经过该排序网络后，得到一个最长上升子序列长度大于等于$n$的个数。$n\le 50, m\le 10$
题解 : 长度为$n$的最长上升子序列长度大于等于$n$的排列个数为$(n-2)*n+2$个，然后DFS找到初始排列即可，不同的最终排列得到的初始合法排列不会重复（因为相同排列在经过相同排序网络应得到相同排列）。

ICPC 2018 徐州 M Rikka with Illuminations

题意 : 给定$n$个点的凸包，有$m$盏灯，询问最少几盏灯能覆盖整个凸包。$n,m\le1000$
题解 : 和SRM 655 Hard BichromeSky意外地一样呢，求切线，转换为区间覆盖。这里不需要像那个题统计所有情况，枚举环上断开，每次排序贪心即可。$O(n^2logn)$

网络赛

2019 徐州网络赛 F Little M’s attack plan

题意 : 给定一棵树，多次询问距离树上某点距离小于等于$k$的权值和。$n\le 10^6, q\le 5000, k\le 100$
题解 : 定义以$u$为根的子树中前$k$层的权值和为$f(u,k)$。询问距离一个点$u$距离为$k$的全值和为$f(u,k)+\sum_{i=1}^{k}f(fa^i,k-i+1)-f(fa^{i-1},k-i)$。
求$f(u,k)$时，维护每个深度的前缀和，在DFS离开和到达这个点$u$时的$sum[dep[u],dep[u]+k]$差即可。
复杂度$O(qk\log{n})$

PREVIOUSWork for Open Source Community Using Git

NEXTMonte Carlo Methods for Volumetric Light Transport Simulation